 |
Geo Stars Library
0.9.3
Geodetic and Astrometry library
|
 |
Geo Stars Library
0.9.3
Geodetic and Astrometry library
|
#include <time.h>

Go to the source code of this file.
Data Structures | |
| struct | GEO_ELLIPSOID |
| struct | GEO_DATUM |
| struct | GEO_LOCATION |
| struct | WMM_DATA |
Macros | |
| #define | GEOSTARSLIB_VERSION 0.9 |
| #define | DLL_API |
| DLL calling convention. More... | |
| #define | DLL_CALLCONV |
| DLL calling convention. More... | |
| #define | GEO_DATUM_DEFAULT 0 |
| Default datum (WGS84) More... | |
| #define | GEO_DATUM_AA 1 |
| Datum : Airy 1830. More... | |
| #define | GEO_DATUM_AN 2 |
| Datum : Australian National. More... | |
| #define | GEO_DATUM_BR 3 |
| Datum : Bessel 1841. More... | |
| #define | GEO_DATUM_BN 4 |
| Datum : Bessel 1841 (Namibia) More... | |
| #define | GEO_DATUM_CC 5 |
| Datum : Clarke 1866. More... | |
| #define | GEO_DATUM_CD 6 |
| Datum : Clarke 1880. More... | |
| #define | GEO_DATUM_EB 7 |
| Datum : Everest (Brunei, E. Malaysia (Sabah and Sarawak)) More... | |
| #define | GEO_DATUM_EA 8 |
| Datum : Everest 1830. More... | |
| #define | GEO_DATUM_EC 9 |
| Datum : Everest 1956 (India and Nepal) More... | |
| #define | GEO_DATUM_EF 10 |
| Datum : Everest (Pakistan) More... | |
| #define | GEO_DATUM_EE 11 |
| Datum : Everest 1948 (W. Malaysia and Singapore) More... | |
| #define | GEO_DATUM_ED 12 |
| Datum : Everest 1969 (W. Malaysia) More... | |
| #define | GEO_DATUM_RF 13 |
| Datum : Geodetic Reference System 1980 (GRS80) More... | |
| #define | GEO_DATUM_HE 14 |
| Datum : Helmert 1906. More... | |
| #define | GEO_DATUM_HO 15 |
| Datum : Hough 1960. More... | |
| #define | GEO_DATUM_ID 16 |
| Datum : Indonesian 1974. More... | |
| #define | GEO_DATUM_IN 17 |
| Datum : International 1924. More... | |
| #define | GEO_DATUM_KA 18 |
| Datum : Krassovsky 1940. More... | |
| #define | GEO_DATUM_AM 19 |
| Datum : Modified Airy. More... | |
| #define | GEO_DATUM_FA 20 |
| Datum : Modified Fischer 1960. More... | |
| #define | GEO_DATUM_SA 21 |
| Datum : South American 1969. More... | |
| #define | GEO_DATUM_WD 22 |
| Datum : WGS 1972. More... | |
| #define | GEO_DATUM_WE 23 |
| Datum : WGS 1984. More... | |
| #define | GEO_DATUM_83 24 |
| Datum : NAD 1983 (same as GRS80) More... | |
| #define | GEO_DATUM_MAX GEO_DATUM_83 |
| #define | GEO_OK 0 |
| Geo Library return OK. More... | |
| #define | GEO_ERROR 1 |
| Geo Library return ERROR. More... | |
| #define | M_PI 3.14159265358979323846 |
Value of 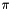 . More... . More... | |
| #define | TWO_PI (2.0*M_PI) |
| #define | sqr(n) (n*n) |
| #define | cube(n) (n*n*n) |
| #define | DEG_TO_RAD (M_PI/180.0) |
| Degrees to Radians conversion factor. More... | |
| #define | RAD_TO_DEG (180.0/M_PI) |
| Radians to Degrees conversion factor. More... | |
| #define | MIN_TO_DEG (1.0/60.0) |
| Minutes to Degrees conversion factor. More... | |
| #define | DEG_TO_MIN (60.0) |
| Degrees to Minutes conversion factor. More... | |
| #define | SEC_TO_DEG (1.0/3600.0) |
| Seconds to Degrees conversion factor. More... | |
| #define | SIN_1 (sin(SEC_TO_DEG*DEG_TO_RAD)) |
| #define | CIRCLE (360.0) |
| #define | HALF_CIRCLE (CIRCLE / 2.0) |
| #define | DELTA_LAT (0.000000001) |
| Delta Lat for EFG2LLH routines. More... | |
| #define | SOLAR_RADIUS 0.2666 |
| #define | SOLAR_DIAMETER (2.0 * SOLAR_SEMIDIAMETER) |
| #define | GEO_B(a, f) (a*(1.0-(1.0/f))) |
| #define | GEO_FL(f) (1.0/f) |
| #define | GEO_E2(a, f) (((a*a) - ((GEO_B(a,f))*(GEO_B(a,f))))/(a*a)) |
| #define | GEO_E2P(a, f) (((a*a) - ((GEO_B(a,f))*(GEO_B(a,f))))/((GEO_B(a,f))*(GEO_B(a,f)))) |
| #define | GEO_WGS84_a (6378137.0) |
| #define | GEO_WGS84_b GEO_B(GEO_WGS84_a,298.257223563) |
| #define | GEO_WGS84_fl GEO_FL(298.257223563) |
| #define | GEO_WGS84_e2 GEO_E2(GEO_WGS84_a,298.257223563) |
| #define | GEO_WGS84_ee2 GEO_E2P(GEO_WGS84_a,298.257223563) |
| #define | GEO_LAT 0 |
| Latitude. More... | |
| #define | GEO_LON 1 |
| Longitude. More... | |
| #define | GEO_HGT 2 |
| Height ( METERS ) More... | |
| #define | GEO_X 0 |
| X or East coordinate of the local tangential plane ( METERS ) More... | |
| #define | GEO_Y 1 |
| Y or North coordinate of the local tangential plane ( METERS ) More... | |
| #define | GEO_Z 2 |
| Z or Up coordinate of the local tangential plane ( METERS ) More... | |
| #define | GEO_E 0 |
| E coordinate of Earth Fixed Geocentric coordinate ( METERS ) More... | |
| #define | GEO_F 1 |
| F coordinate of Earth Fixed Geocentric coordinate ( METERS ) More... | |
| #define | GEO_G 2 |
| G coordinate of Earth Fixed Geocentric coordinate ( METERS ) More... | |
| #define | GEO_RNG 0 |
| Slant range ( METERS ) More... | |
| #define | GEO_AZ 1 |
| Azimuth, clockwise from north. More... | |
| #define | GEO_EL 2 |
| Elevation, from horizon (0) up. More... | |
| #define | GEO_SZ_ELLIPSOID_NAME 82 |
| Max size of the Ellipsoid name field. More... | |
| #define | GEO_EFG2LLH_MAX_ITS 10 |
| Max iterations allowed in the efg2llh routines. More... | |
| #define | GEO_EFG2LLH_ACCURACY_METER 0.00001 |
| Use Meter Accuracy in Efg2Llh routines. More... | |
| #define | GEO_EFG2LLH_ACCURACY_CM 0.0000001 |
| Use Centimeter Accuracy in Efg2Llh routines. More... | |
| #define | GEO_EFG2LLH_ACCURACY_MM 0.00000001 |
| Use Millimeter Accuracy in Efg2Llh routines. More... | |
| #define | GEO_EFG2LLH_ACCURACY_MAX 0.0 |
| Use Maximum Accuracy in Efg2Llh routines. More... | |
| #define | GEO_EFG2LLH_ACCURACY GEO_EFG2LLH_ACCURACY_MM |
| Millimeter accuracy is default. More... | |
| #define | MAX(a, b) ((a>b)?(a):(b)) |
Functions | |
| void | geoGetEllipsoid (double *a, double *b, double *e2, double *ee2, double *f, int datum) |
| This routine computes essential datum values from basic parameters obtained from the ellips structure. More... | |
| int | geoInitDatum (GEO_DATUM *d, int datum) |
| int | geoInitLocation (GEO_LOCATION *l, double lat, double lon, double hgt, int datum, char *name) |
| This routine needs to be called when a site (or location) is initialized. Several of the routines use the information in the structure that this routine fills. More... | |
| int | geoInitLocation2 (GEO_LOCATION *l, double lat, double lon, double hgt, const GEO_DATUM *datum, const char *name) |
| void | geoSetTimeZone (GEO_LOCATION *l, double tz, int dst) |
| int | geoSunAzElNow (GEO_LOCATION *loc, double *az, double *el) |
| this routine uses ANSI C time routines to obtain the current time and then get the az and el of the sun at this location More... | |
| int | geoSunAzEltm (GEO_LOCATION *loc, double *az, double *el, struct tm *newtime) |
| this routine ingests an ANSI C time structure and then gets the az and el of the sun at this location based on this time. More... | |
| int | geoSunAzElJD (GEO_LOCATION *loc, double *az, double *el, double tjd_now) |
| This routine uses a previously determined Julian date and then gets the Az and El of the sun at this location based on the Julian date. More... | |
| int | geoGetSunError (void) |
| int | geoGettm (int part) |
| double | geoSunNowEl (double lat, double lon, double hgt) |
| this routine uses the location and current time to get the elevation of the sun at this location More... | |
| double | geoSunNowAz (double lat, double lon, double hgt) |
| this routine uses the location and current time to get the azimuth of the sun at this location More... | |
| double | geoVersion (void) |
| This function returns the version of the GeoStarsLib. More... | |
| int | geoEfg2XyzDiff (GEO_LOCATION *src_desc, GEO_LOCATION *tgt_desc, double xyz_disp[]) |
| This function returns the XYZ offset of the target point with respect to the source point, given the Earth Fixed Geodetic coordinates of the points. The EFG coordinates for the source must appear in the GEO_LOCATION record, which must be built previous to the call to this procedure. More... | |
| int | geoEfg2XyzDiff_packed (GEO_LOCATION *src_desc, int count, double efg_xyz[]) |
| This function returns the XYZ offset of the target point with respect to the source point, given the Earth Fixed Geodetic coordinates of the points. The EFG coordinates for the source must appear in the GEO_LOCATION record, which must be built previous to the call to this procedure. More... | |
| void | geoRae2Efg (GEO_LOCATION *loc, double aer_in[], double efg_out[]) |
| Ingests Range, Azimuth, Elevation and site info and returns the EFG coordinates that the RAE points to. More... | |
| void | geoEfg2Llh (int datum, double efg[], double *lat, double *lon, double *hgt) |
This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| void | geoEfg2Llh_packed (const GEO_DATUM *datum, int count, double efg_llh[]) |
| double | geoEfg2Lat (int datum, double e, double f, double g) |
| double | geoEfg2Lon (int datum, double e, double f, double g) |
| double | geoEfg2Hgt (int datum, double e, double f, double g) |
| void | geoEfg2Llh_hm (int datum, double efg[], double *lat, double *lon, double *hgt) |
Hirvonen & Moritz Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_hm (int datum, double e, double f, double g) |
| double | geoEfg2Lon_hm (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_hm (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_hm_its (int datum, double e, double f, double g) |
| void | geoEfg2Llh_torge (int datum, double efg[], double *lat, double *lon, double *hgt) |
Torge Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_torge (int datum, double e, double f, double g) |
| double | geoEfg2Lon_torge (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_torge (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_torge_its (int datum, double e, double f, double g) |
| void | geoEfg2Llh_bowring (int datum, double efg[], double *lat, double *lon, double *hgt) |
Bowring Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_bowring (int datum, double e, double f, double g) |
| double | geoEfg2Lon_bowring (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_bowring (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_bowring_its (int datum, double e, double f, double g) |
| void | geoEfg2Llh_aa (int datum, double efg[], double *lat, double *lon, double *hgt) |
Astronomical Almanac 2002 Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_aa (int datum, double e, double f, double g) |
| double | geoEfg2Lon_aa (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_aa (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_aa_its (int datum, double e, double f, double g) |
| void | geoEfg2Llh_borkowski (int datum, double efg[], double *lat, double *lon, double *hgt) |
Borkowski Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_borkowski (int datum, double e, double f, double g) |
| double | geoEfg2Lon_borkowski (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_borkowski (int datum, double e, double f, double g) |
| void | geoEfg2Llh_vermeille (int datum, double efg[], double *lat, double *lon, double *hgt) |
Vermeille Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_vermeille (int datum, double e, double f, double g) |
| double | geoEfg2Lon_vermeille (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_vermeille (int datum, double e, double f, double g) |
| void | geoEfg2Llh_heikkinen (int datum, double efg[], double *lat, double *lon, double *hgt) |
heikkinen Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_heikkinen (int datum, double e, double f, double g) |
| double | geoEfg2Lon_heikkinen (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_heikkinen (int datum, double e, double f, double g) |
| void | geoEfg2Llh_toms (int datum, double efg[], double *lat, double *lon, double *hgt) |
| double | geoEfg2Lat_toms (int datum, double e, double f, double g) |
| double | geoEfg2Lon_toms (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_toms (int datum, double e, double f, double g) |
| int | geoEfg2LlhGetIts (void) |
| int | geoSetAccuracy (double acc) |
| This routine will set the accuracy of the iterative Efg2Llh routines (geoEfg2Llh_hm, geoEfg2Llh_torge, geoEfg2Llh_bowring, geoEfg2Llh_aa) More... | |
| void | geoEfg2Llh_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| void | geoEfg2Llh_fast_packed (const GEO_DATUM *datum, int count, double efg_llh[]) |
| void | geoEfg2Llh_fast_packed2 (const GEO_DATUM *datum, int count, double efg_in[], double llh_out[]) |
| double | geoEfg2Lat_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_hm_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Hirvonen & Moritz Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_hm_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_hm_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_hm_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_torge_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Torge Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_torge_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_torge_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_torge_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_bowring_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Bowring Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_bowring_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_bowring_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_bowring_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_aa_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Astronomical Almanac 2002 Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_aa_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_aa_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_aa_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_borkowski_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Borkowski Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_borkowski_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_borkowski_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_borkowski_fast (int datum, double e, double f, double g) |
| void | geoEfg2Llh_vermeille_fast (int datum, double efg[], double *lat, double *lon, double *hgt) |
Vermeille Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ). More... ). More... | |
| double | geoEfg2Lat_vermeille_fast (int datum, double e, double f, double g) |
| double | geoEfg2Lon_vermeille_fast (int datum, double e, double f, double g) |
| double | geoEfg2Hgt_vermeille_fast (int datum, double e, double f, double g) |
| void | geoLlh2Efg (double lat, double lon, double height, int datum, double *e, double *f, double *g) |
This routine will convert geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). More... ) into earth centered Cartesian coordinates (E,F,G). More... | |
| void | geoLlh2Efg_packed (GEO_DATUM *datum, int count, double llh_efg[]) |
This routine will convert geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). More... ) into earth centered Cartesian coordinates (E,F,G). More... | |
| double | geoLlh2E (double lat, double lon, double height, int datum) |
This routine will convert geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the E component. More... ) into earth centered Cartesian coordinates (E,F,G). This returns the E component. More... | |
| double | geoLlh2F (double lat, double lon, double height, int datum) |
This routine will convert geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the F component. More... ) into earth centered Cartesian coordinates (E,F,G). This returns the F component. More... | |
| double | geoLlh2G (double lat, double lon, double height, int datum) |
This routine will convert geodetic coordinates (latitude  , longitude , longitude  , and ellipsoid height , and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the G component. More... ) into earth centered Cartesian coordinates (E,F,G). This returns the G component. More... | |
| double | geoLlh2DiffX (double lat1, double lon1, double hgt1, int datum1, double lat2, double lon2, double hgt2, int datum2) |
| double | geoLlh2DiffY (double lat1, double lon1, double hgt1, int datum1, double lat2, double lon2, double hgt2, int datum2) |
| double | geoLlh2DiffZ (double lat1, double lon1, double hgt1, int datum1, double lat2, double lon2, double hgt2, int datum2) |
| void | geoXyz2Rae (double xyz_in[], double rae_out[]) |
| Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2Rae calculates the range, azimuth, and elevation to that point. More... | |
| void | geoXyz2Rae_packed (int count, double xyz_rae[]) |
| Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2Rae calculates the range, azimuth, and elevation to that point. More... | |
| double | geoXyz2R (double x, double y, double z) |
| Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the range to that point. More... | |
| double | geoXyz2A (double x, double y, double z) |
| Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the azimuth to that point. More... | |
| double | geoXyz2E (double x, double y, double z) |
| Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the elevation angle to that point. More... | |
| void | geoXyz2Efg (GEO_LOCATION *loc, double xyz_in[], double efg_out[]) |
| Ingests X, Y, Z, and site info and returns the EFG coordinates. More... | |
| void | geoXyz2Efg_packed (GEO_LOCATION *loc, int size, double xyz_efg[]) |
| This routine takes site info and iterates over count vertices in the tightly packed array xyz_efg converting it from cartesian XYZ into geocentric EFG coordinates. More... | |
| void | geoRae2Xyz (double rae_in[], double xyz_out[]) |
| This routine converts from Range, Azimuth, and Elevation into Cartesian coordinates X,Y,Z. More... | |
| void | geoRae2Xyz_packed (int size, double rae_xyz[]) |
| This routine iterates over count vertices in the array rae_xyz converting it from Range, Azimuth, and Elevation into Cartesian coordinates X,Y,Z. More... | |
| double | geoRads2Decdms (double rads) |
| Convert radians to decimal degrees, minutes, and seconds ("dddmmss.s"). More... | |
| void | geoRads2Dms (double rads, double *deg, double *min, double *sec, double *dir) |
| Converts radians to degrees minutes seconds. More... | |
| double | geoRads2DD (double rads) |
| Converts radians to Decimal Degrees. More... | |
| double | geoDecdms2Rads (double in) |
| Convert decimal degrees, minutes, and seconds ("dmmss.s") to radians. More... | |
| double | geoDms2DD (double deg, double min, double sec, char *sign) |
| Converts degrees minutes seconds to Decimal Degrees. More... | |
| double | geoDms2Rads (double deg, double min, double sec, char *sign) |
| Converts degrees minutes seconds to radians. More... | |
| void | geoDD2Dms (double dd, double *deg, double *min, double *sec, double *dir) |
| Converts Decimal Degrees to degrees minutes seconds. More... | |
| double | geoDD2Rads (double dd) |
| Converts Decimal Degrees to radians. More... | |
| double | geoDD2Deg (double dd) |
| double | geoDD2Min (double dd) |
| double | geoDD2Sec (double dd) |
| int | geomg1 (double alt, double glat, double glon, double time, double *dec, double *dip, double *ti, double *gv) |
| int | geoMag (double alt, double glat, double glon, double time, double *dec, double *dip, double *ti, double *gv, double *adec, double *adip, double *ati, double *x, double *y, double *z, double *h, double *ax, double *ay, double *az, double *ah) |
| This routine computes all of the relevant geomagnetic data. More... | |
| int | geoMagGetDec (double lat, double lon, double hgt, int month, int day, int year, double *dec) |
| This routine computes magnetic declination. More... | |
| double | geoMagGetDecRet (double lat, double lon, double hgt, int month, int day, int year) |
| This routine computes and returns magnetic declination for a specific date. More... | |
| int | geoMagFillDec (GEO_LOCATION *l, double *dec) |
| double | geoMagGetDecNow (double lat, double lon, double hgt) |
| This routine computes magnetic declination for now time. More... | |
| int | geoSun (GEO_LOCATION *loc, struct tm *newtime, double *az, double *el) |
| int | geoSunM (GEO_LOCATION *loc, struct tm *newtime, double *az, double *el) |
| int | geoSunAA (GEO_LOCATION *loc, struct tm *newtime, double *az, double *el) |
| int | geoSunPosition (GEO_LOCATION *loc, double *az, double *el) |
| this routine uses ANSI C time routines to obtain the current time and then get the az and el of the sun at this location More... | |
Variables | |
| double | geoAccuracy |
| GEO_ELLIPSOID | ellips [] |
| This structure array contains the all of the ellipsoids used in this library. More... | |
| int | geoSunError |
rief This file has all of the definitions for the Geo Library: geoEllips, geoAstro, geoPoint, and geoMag.
Definition in file geoStars.h.
| #define CIRCLE (360.0) |
Definition at line 600 of file geoStars.h.
Referenced by geomg1().
Definition at line 592 of file geoStars.h.
Referenced by geoEfg2Llh(), geoEfg2Llh_borkowski(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_toms(), and geoEfg2Llh_vermeille_fast().
| #define DEG_TO_MIN (60.0) |
Degrees to Minutes conversion factor.
Definition at line 597 of file geoStars.h.
Referenced by geoMag().
| #define DEG_TO_RAD (M_PI/180.0) |
Degrees to Radians conversion factor.
Definition at line 594 of file geoStars.h.
Referenced by geoDD2Rads(), geoDecdms2Rads(), geoDms2Rads(), geoInitLocation(), geoMag(), geomg1(), geoSun(), geoSunAA(), and geoSunM().
| #define DELTA_LAT (0.000000001) |
Delta Lat for EFG2LLH routines.
Definition at line 602 of file geoStars.h.
| #define DLL_API |
DLL calling convention.
Definition at line 529 of file geoStars.h.
| #define DLL_CALLCONV |
DLL calling convention.
Definition at line 530 of file geoStars.h.
| #define GEO_AZ 1 |
Azimuth, clockwise from north.
Definition at line 665 of file geoStars.h.
Referenced by geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2A(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEO_B | ( | a, | |
| f | |||
| ) | (a*(1.0-(1.0/f))) |
All geodetic datums and ellipsoids are defined by flattening 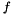 and the major axis
and the major axis 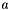 . From these parameters, the other axis and eccentricity can be calculated. Minor Axis
. From these parameters, the other axis and eccentricity can be calculated. Minor Axis  of the Earth is calculated from the Inverse Flattening
of the Earth is calculated from the Inverse Flattening 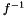 and the Major Axis
and the Major Axis 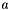 .
.
Where
![\[b={a (1- \frac{1}{f^{-1}})}\]](form_32.png)
Definition at line 640 of file geoStars.h.
Referenced by geoGetEllipsoid(), and geomg1().
| #define GEO_DATUM_83 24 |
Datum : NAD 1983 (same as GRS80)
Definition at line 574 of file geoStars.h.
| #define GEO_DATUM_AA 1 |
Datum : Airy 1830.
Definition at line 551 of file geoStars.h.
| #define GEO_DATUM_AM 19 |
Datum : Modified Airy.
Definition at line 569 of file geoStars.h.
| #define GEO_DATUM_AN 2 |
Datum : Australian National.
Definition at line 552 of file geoStars.h.
| #define GEO_DATUM_BN 4 |
Datum : Bessel 1841 (Namibia)
Definition at line 554 of file geoStars.h.
| #define GEO_DATUM_BR 3 |
Datum : Bessel 1841.
Definition at line 553 of file geoStars.h.
| #define GEO_DATUM_CC 5 |
Datum : Clarke 1866.
Definition at line 555 of file geoStars.h.
| #define GEO_DATUM_CD 6 |
Datum : Clarke 1880.
Definition at line 556 of file geoStars.h.
| #define GEO_DATUM_DEFAULT 0 |
Default datum (WGS84)
Definition at line 550 of file geoStars.h.
Referenced by geoSunNowAz(), and geoSunNowEl().
| #define GEO_DATUM_EA 8 |
Datum : Everest 1830.
Definition at line 558 of file geoStars.h.
| #define GEO_DATUM_EB 7 |
Datum : Everest (Brunei, E. Malaysia (Sabah and Sarawak))
Definition at line 557 of file geoStars.h.
| #define GEO_DATUM_EC 9 |
Datum : Everest 1956 (India and Nepal)
Definition at line 559 of file geoStars.h.
| #define GEO_DATUM_ED 12 |
Datum : Everest 1969 (W. Malaysia)
Definition at line 562 of file geoStars.h.
| #define GEO_DATUM_EE 11 |
Datum : Everest 1948 (W. Malaysia and Singapore)
Definition at line 561 of file geoStars.h.
| #define GEO_DATUM_EF 10 |
Datum : Everest (Pakistan)
Definition at line 560 of file geoStars.h.
| #define GEO_DATUM_FA 20 |
Datum : Modified Fischer 1960.
Definition at line 570 of file geoStars.h.
| #define GEO_DATUM_HE 14 |
Datum : Helmert 1906.
Definition at line 564 of file geoStars.h.
| #define GEO_DATUM_HO 15 |
Datum : Hough 1960.
Definition at line 565 of file geoStars.h.
| #define GEO_DATUM_ID 16 |
Datum : Indonesian 1974.
Definition at line 566 of file geoStars.h.
| #define GEO_DATUM_IN 17 |
Datum : International 1924.
Definition at line 567 of file geoStars.h.
| #define GEO_DATUM_KA 18 |
Datum : Krassovsky 1940.
Definition at line 568 of file geoStars.h.
| #define GEO_DATUM_MAX GEO_DATUM_83 |
Definition at line 577 of file geoStars.h.
Referenced by geoInitLocation().
| #define GEO_DATUM_RF 13 |
Datum : Geodetic Reference System 1980 (GRS80)
Definition at line 563 of file geoStars.h.
| #define GEO_DATUM_SA 21 |
Datum : South American 1969.
Definition at line 571 of file geoStars.h.
| #define GEO_DATUM_WD 22 |
Datum : WGS 1972.
Definition at line 572 of file geoStars.h.
| #define GEO_DATUM_WE 23 |
| #define GEO_E 0 |
E coordinate of Earth Fixed Geocentric coordinate ( METERS )
Definition at line 661 of file geoStars.h.
Referenced by geoEfg2Hgt(), geoEfg2Hgt_aa(), geoEfg2Hgt_aa_fast(), geoEfg2Hgt_aa_its(), geoEfg2Hgt_borkowski(), geoEfg2Hgt_borkowski_fast(), geoEfg2Hgt_bowring(), geoEfg2Hgt_bowring_fast(), geoEfg2Hgt_bowring_its(), geoEfg2Hgt_fast(), geoEfg2Hgt_heikkinen(), geoEfg2Hgt_hm(), geoEfg2Hgt_hm_fast(), geoEfg2Hgt_hm_its(), geoEfg2Hgt_toms(), geoEfg2Hgt_torge(), geoEfg2Hgt_torge_fast(), geoEfg2Hgt_torge_its(), geoEfg2Hgt_vermeille(), geoEfg2Hgt_vermeille_fast(), geoEfg2Lat(), geoEfg2Lat_aa(), geoEfg2Lat_aa_fast(), geoEfg2Lat_borkowski(), geoEfg2Lat_borkowski_fast(), geoEfg2Lat_bowring(), geoEfg2Lat_bowring_fast(), geoEfg2Lat_fast(), geoEfg2Lat_heikkinen(), geoEfg2Lat_hm(), geoEfg2Lat_hm_fast(), geoEfg2Lat_torge(), geoEfg2Lat_torge_fast(), geoEfg2Lat_vermeille(), geoEfg2Lat_vermeille_fast(), geoEfg2Llh(), geoEfg2Llh_aa(), geoEfg2Llh_aa_fast(), geoEfg2Llh_borkowski(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_heikkinen(), geoEfg2Llh_hm(), geoEfg2Llh_hm_fast(), geoEfg2Llh_toms(), geoEfg2Llh_torge(), geoEfg2Llh_torge_fast(), geoEfg2Llh_vermeille(), geoEfg2Llh_vermeille_fast(), geoEfg2Lon(), geoEfg2Lon_aa(), geoEfg2Lon_aa_fast(), geoEfg2Lon_borkowski(), geoEfg2Lon_borkowski_fast(), geoEfg2Lon_bowring(), geoEfg2Lon_bowring_fast(), geoEfg2Lon_fast(), geoEfg2Lon_heikkinen(), geoEfg2Lon_hm(), geoEfg2Lon_hm_fast(), geoEfg2Lon_toms(), geoEfg2Lon_torge(), geoEfg2Lon_torge_fast(), geoEfg2Lon_vermeille(), geoEfg2Lon_vermeille_fast(), geoEfg2XyzDiff_packed(), geoInitLocation(), geoLlh2Efg_packed(), geoRae2Efg(), geoXyz2Efg(), and geoXyz2Efg_packed().
Eccentricity Squared 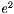 is computed in the following manner:
is computed in the following manner:
![\[e^2 = \frac{a^2 - b^2}{a^2}\]](form_10.png)
Definition at line 642 of file geoStars.h.
Referenced by geoGetEllipsoid().
Eccentricity Squared Prime 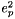 is computed in the following manner:
is computed in the following manner:
![\[e^2_p = \frac{a^2 - b^2}{b^2}\]](form_12.png)
Definition at line 643 of file geoStars.h.
Referenced by geoGetEllipsoid().
| #define GEO_EFG2LLH_ACCURACY GEO_EFG2LLH_ACCURACY_MM |
Millimeter accuracy is default.
Definition at line 677 of file geoStars.h.
| #define GEO_EFG2LLH_ACCURACY_CM 0.0000001 |
Use Centimeter Accuracy in Efg2Llh routines.
Definition at line 674 of file geoStars.h.
| #define GEO_EFG2LLH_ACCURACY_MAX 0.0 |
Use Maximum Accuracy in Efg2Llh routines.
Definition at line 676 of file geoStars.h.
| #define GEO_EFG2LLH_ACCURACY_METER 0.00001 |
Use Meter Accuracy in Efg2Llh routines.
Definition at line 673 of file geoStars.h.
| #define GEO_EFG2LLH_ACCURACY_MM 0.00000001 |
Use Millimeter Accuracy in Efg2Llh routines.
Definition at line 675 of file geoStars.h.
| #define GEO_EFG2LLH_MAX_ITS 10 |
Max iterations allowed in the efg2llh routines.
Definition at line 672 of file geoStars.h.
Referenced by geoEfg2Llh_aa(), geoEfg2Llh_bowring(), geoEfg2Llh_hm(), and geoEfg2Llh_torge().
| #define GEO_EL 2 |
Elevation, from horizon (0) up.
Definition at line 666 of file geoStars.h.
Referenced by geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2E(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEO_ERROR 1 |
Geo Library return ERROR.
Definition at line 582 of file geoStars.h.
Referenced by geoInitLocation(), geoSetAccuracy(), and geoSunAzElJD().
| #define GEO_F 1 |
F coordinate of Earth Fixed Geocentric coordinate ( METERS )
Definition at line 662 of file geoStars.h.
Referenced by geoEfg2Hgt(), geoEfg2Hgt_aa(), geoEfg2Hgt_aa_fast(), geoEfg2Hgt_aa_its(), geoEfg2Hgt_borkowski(), geoEfg2Hgt_borkowski_fast(), geoEfg2Hgt_bowring(), geoEfg2Hgt_bowring_fast(), geoEfg2Hgt_bowring_its(), geoEfg2Hgt_fast(), geoEfg2Hgt_heikkinen(), geoEfg2Hgt_hm(), geoEfg2Hgt_hm_fast(), geoEfg2Hgt_hm_its(), geoEfg2Hgt_toms(), geoEfg2Hgt_torge(), geoEfg2Hgt_torge_fast(), geoEfg2Hgt_torge_its(), geoEfg2Hgt_vermeille(), geoEfg2Hgt_vermeille_fast(), geoEfg2Lat(), geoEfg2Lat_aa(), geoEfg2Lat_aa_fast(), geoEfg2Lat_borkowski(), geoEfg2Lat_borkowski_fast(), geoEfg2Lat_bowring(), geoEfg2Lat_bowring_fast(), geoEfg2Lat_fast(), geoEfg2Lat_heikkinen(), geoEfg2Lat_hm(), geoEfg2Lat_hm_fast(), geoEfg2Lat_torge(), geoEfg2Lat_torge_fast(), geoEfg2Lat_vermeille(), geoEfg2Lat_vermeille_fast(), geoEfg2Llh(), geoEfg2Llh_aa(), geoEfg2Llh_aa_fast(), geoEfg2Llh_borkowski(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_heikkinen(), geoEfg2Llh_hm(), geoEfg2Llh_hm_fast(), geoEfg2Llh_toms(), geoEfg2Llh_torge(), geoEfg2Llh_torge_fast(), geoEfg2Llh_vermeille(), geoEfg2Llh_vermeille_fast(), geoEfg2Lon(), geoEfg2Lon_aa(), geoEfg2Lon_aa_fast(), geoEfg2Lon_borkowski(), geoEfg2Lon_borkowski_fast(), geoEfg2Lon_bowring(), geoEfg2Lon_bowring_fast(), geoEfg2Lon_fast(), geoEfg2Lon_heikkinen(), geoEfg2Lon_hm(), geoEfg2Lon_hm_fast(), geoEfg2Lon_toms(), geoEfg2Lon_torge(), geoEfg2Lon_torge_fast(), geoEfg2Lon_vermeille(), geoEfg2Lon_vermeille_fast(), geoEfg2XyzDiff_packed(), geoInitLocation(), geoLlh2Efg_packed(), geoRae2Efg(), geoXyz2Efg(), and geoXyz2Efg_packed().
| #define GEO_FL | ( | f) | (1.0/f) |
Since the Geo Library ellips structure uses inverse flattening 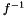 then flattening can be calculated by
then flattening can be calculated by
![\[\frac{1}{f^{-1}}\]](form_33.png)
Duh!
Definition at line 641 of file geoStars.h.
Referenced by geoGetEllipsoid().
| #define GEO_G 2 |
G coordinate of Earth Fixed Geocentric coordinate ( METERS )
Definition at line 663 of file geoStars.h.
Referenced by geoEfg2Hgt(), geoEfg2Hgt_aa(), geoEfg2Hgt_aa_fast(), geoEfg2Hgt_aa_its(), geoEfg2Hgt_borkowski(), geoEfg2Hgt_borkowski_fast(), geoEfg2Hgt_bowring(), geoEfg2Hgt_bowring_fast(), geoEfg2Hgt_bowring_its(), geoEfg2Hgt_fast(), geoEfg2Hgt_heikkinen(), geoEfg2Hgt_hm(), geoEfg2Hgt_hm_fast(), geoEfg2Hgt_hm_its(), geoEfg2Hgt_toms(), geoEfg2Hgt_torge(), geoEfg2Hgt_torge_fast(), geoEfg2Hgt_torge_its(), geoEfg2Hgt_vermeille(), geoEfg2Hgt_vermeille_fast(), geoEfg2Lat(), geoEfg2Lat_aa(), geoEfg2Lat_aa_fast(), geoEfg2Lat_borkowski(), geoEfg2Lat_borkowski_fast(), geoEfg2Lat_bowring(), geoEfg2Lat_bowring_fast(), geoEfg2Lat_fast(), geoEfg2Lat_heikkinen(), geoEfg2Lat_hm(), geoEfg2Lat_hm_fast(), geoEfg2Lat_torge(), geoEfg2Lat_torge_fast(), geoEfg2Lat_vermeille(), geoEfg2Lat_vermeille_fast(), geoEfg2Llh(), geoEfg2Llh_aa(), geoEfg2Llh_aa_fast(), geoEfg2Llh_borkowski(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_heikkinen(), geoEfg2Llh_hm(), geoEfg2Llh_hm_fast(), geoEfg2Llh_toms(), geoEfg2Llh_torge(), geoEfg2Llh_torge_fast(), geoEfg2Llh_vermeille(), geoEfg2Llh_vermeille_fast(), geoEfg2Lon(), geoEfg2Lon_aa(), geoEfg2Lon_aa_fast(), geoEfg2Lon_borkowski(), geoEfg2Lon_borkowski_fast(), geoEfg2Lon_bowring(), geoEfg2Lon_bowring_fast(), geoEfg2Lon_fast(), geoEfg2Lon_heikkinen(), geoEfg2Lon_hm(), geoEfg2Lon_hm_fast(), geoEfg2Lon_toms(), geoEfg2Lon_torge(), geoEfg2Lon_torge_fast(), geoEfg2Lon_vermeille(), geoEfg2Lon_vermeille_fast(), geoEfg2XyzDiff_packed(), geoInitLocation(), geoLlh2Efg_packed(), geoRae2Efg(), geoXyz2Efg(), and geoXyz2Efg_packed().
| #define GEO_HGT 2 |
| #define GEO_LAT 0 |
| #define GEO_LON 1 |
| #define GEO_OK 0 |
Geo Library return OK.
Definition at line 581 of file geoStars.h.
Referenced by geoEfg2XyzDiff(), geoEfg2XyzDiff_packed(), geoInitLocation(), geoMag(), geoMagFillDec(), geoMagGetDec(), geomg1(), geoSetAccuracy(), geoSun(), geoSunAzElJD(), geoSunM(), and geoSunPosition().
| #define GEO_RNG 0 |
Slant range ( METERS )
Definition at line 664 of file geoStars.h.
Referenced by geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2R(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEO_SZ_ELLIPSOID_NAME 82 |
Max size of the Ellipsoid name field.
Definition at line 669 of file geoStars.h.
| #define GEO_WGS84_a (6378137.0) |
Definition at line 646 of file geoStars.h.
Referenced by geoEfg2Llh_aa_fast(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_hm_fast(), geoEfg2Llh_torge_fast(), and geoEfg2Llh_vermeille_fast().
| #define GEO_WGS84_b GEO_B(GEO_WGS84_a,298.257223563) |
Definition at line 647 of file geoStars.h.
Referenced by geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring_fast(), and geoEfg2Llh_fast().
| #define GEO_WGS84_e2 GEO_E2(GEO_WGS84_a,298.257223563) |
Definition at line 649 of file geoStars.h.
Referenced by geoEfg2Llh_aa_fast(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_hm_fast(), geoEfg2Llh_torge_fast(), and geoEfg2Llh_vermeille_fast().
| #define GEO_WGS84_ee2 GEO_E2P(GEO_WGS84_a,298.257223563) |
Definition at line 650 of file geoStars.h.
Referenced by geoEfg2Llh_bowring_fast(), and geoEfg2Llh_fast().
| #define GEO_WGS84_fl GEO_FL(298.257223563) |
Definition at line 648 of file geoStars.h.
| #define GEO_X 0 |
X or East coordinate of the local tangential plane ( METERS )
Definition at line 658 of file geoStars.h.
Referenced by geoEfg2XyzDiff(), geoEfg2XyzDiff_packed(), geoLlh2DiffX(), geoRae2Efg(), geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2Efg(), geoXyz2Efg_packed(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEO_Y 1 |
Y or North coordinate of the local tangential plane ( METERS )
Definition at line 659 of file geoStars.h.
Referenced by geoEfg2XyzDiff(), geoEfg2XyzDiff_packed(), geoLlh2DiffY(), geoRae2Efg(), geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2Efg(), geoXyz2Efg_packed(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEO_Z 2 |
Z or Up coordinate of the local tangential plane ( METERS )
Definition at line 660 of file geoStars.h.
Referenced by geoEfg2XyzDiff(), geoEfg2XyzDiff_packed(), geoLlh2DiffZ(), geoRae2Efg(), geoRae2Xyz(), geoRae2Xyz_packed(), geoXyz2Efg(), geoXyz2Efg_packed(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define GEOSTARSLIB_VERSION 0.9 |
Definition at line 518 of file geoStars.h.
Referenced by geoVersion().
| #define HALF_CIRCLE (CIRCLE / 2.0) |
Definition at line 601 of file geoStars.h.
Referenced by geomg1().
| #define M_PI 3.14159265358979323846 |
Value of 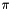 .
.
Definition at line 585 of file geoStars.h.
Referenced by geoSunM(), geoXyz2Rae(), and geoXyz2Rae_packed().
| #define MAX | ( | a, | |
| b | |||
| ) | ((a>b)?(a):(b)) |
Definition at line 791 of file geoStars.h.
| #define MIN_TO_DEG (1.0/60.0) |
Minutes to Degrees conversion factor.
Definition at line 596 of file geoStars.h.
Referenced by geoDms2DD(), and geoDms2Rads().
| #define RAD_TO_DEG (180.0/M_PI) |
Radians to Degrees conversion factor.
Definition at line 595 of file geoStars.h.
Referenced by geoEfg2Lat(), geoEfg2Lat_aa(), geoEfg2Lat_aa_fast(), geoEfg2Lat_borkowski(), geoEfg2Lat_borkowski_fast(), geoEfg2Lat_bowring(), geoEfg2Lat_bowring_fast(), geoEfg2Lat_fast(), geoEfg2Lat_heikkinen(), geoEfg2Lat_hm(), geoEfg2Lat_hm_fast(), geoEfg2Lat_toms(), geoEfg2Lat_torge(), geoEfg2Lat_torge_fast(), geoEfg2Lat_vermeille(), geoEfg2Lat_vermeille_fast(), geoEfg2Lon(), geoEfg2Lon_aa(), geoEfg2Lon_aa_fast(), geoEfg2Lon_borkowski(), geoEfg2Lon_borkowski_fast(), geoEfg2Lon_bowring(), geoEfg2Lon_bowring_fast(), geoEfg2Lon_fast(), geoEfg2Lon_heikkinen(), geoEfg2Lon_hm(), geoEfg2Lon_hm_fast(), geoEfg2Lon_toms(), geoEfg2Lon_torge(), geoEfg2Lon_torge_fast(), geoEfg2Lon_vermeille(), geoEfg2Lon_vermeille_fast(), geomg1(), geoRads2DD(), geoRads2Decdms(), geoRads2Dms(), geoSun(), geoSunAA(), geoSunM(), geoXyz2A(), and geoXyz2E().
| #define SEC_TO_DEG (1.0/3600.0) |
Seconds to Degrees conversion factor.
Definition at line 598 of file geoStars.h.
Referenced by geoDms2DD(), and geoDms2Rads().
| #define SIN_1 (sin(SEC_TO_DEG*DEG_TO_RAD)) |
Definition at line 599 of file geoStars.h.
| #define SOLAR_DIAMETER (2.0 * SOLAR_SEMIDIAMETER) |
Definition at line 607 of file geoStars.h.
| #define SOLAR_RADIUS 0.2666 |
Definition at line 606 of file geoStars.h.
Definition at line 591 of file geoStars.h.
Referenced by geoEfg2Llh(), geoEfg2Llh_aa(), geoEfg2Llh_aa_fast(), geoEfg2Llh_borkowski(), geoEfg2Llh_borkowski_fast(), geoEfg2Llh_bowring(), geoEfg2Llh_bowring_fast(), geoEfg2Llh_fast(), geoEfg2Llh_heikkinen(), geoEfg2Llh_hm(), geoEfg2Llh_hm_fast(), geoEfg2Llh_toms(), geoEfg2Llh_torge(), geoEfg2Llh_torge_fast(), geoEfg2Llh_vermeille(), and geoEfg2Llh_vermeille_fast().
| #define TWO_PI (2.0*M_PI) |
Definition at line 588 of file geoStars.h.
Referenced by fractionalYearRad(), and geoSunM().
| double geoDD2Deg | ( | double | dd) |
Definition at line 888 of file geoPoint.c.
References geoDD2Dms().

| void geoDD2Dms | ( | double | dd, |
| double * | deg, | ||
| double * | min, | ||
| double * | sec, | ||
| double * | dir | ||
| ) |
Converts Decimal Degrees to degrees minutes seconds.
| double | decimal degrees |
| double | deg, min, sec |
| char | dir : -1.0 or 1.0 |
Definition at line 865 of file geoPoint.c.
Referenced by geoDD2Deg(), geoDD2Min(), and geoDD2Sec().
| double geoDD2Min | ( | double | dd) |
Definition at line 894 of file geoPoint.c.
References geoDD2Dms().

| double geoDD2Rads | ( | double | dd) |
Converts Decimal Degrees to radians.
| double | decimal degrees |
Definition at line 849 of file geoPoint.c.
References DEG_TO_RAD.
| double geoDD2Sec | ( | double | dd) |
Definition at line 900 of file geoPoint.c.
References geoDD2Dms().

| double geoDecdms2Rads | ( | double | in) |
Convert decimal degrees, minutes, and seconds ("dmmss.s") to radians.
| double | in; // decimal deg,min,sec |
Definition at line 756 of file geoPoint.c.
References DEG_TO_RAD.
| double geoDms2DD | ( | double | deg, |
| double | min, | ||
| double | sec, | ||
| char * | sign | ||
| ) |
Converts degrees minutes seconds to Decimal Degrees.
| double | deg, min, sec |
| char | sign : N,E,S,W,-,+ |
Definition at line 723 of file geoPoint.c.
References MIN_TO_DEG, and SEC_TO_DEG.
| double geoDms2Rads | ( | double | deg, |
| double | min, | ||
| double | sec, | ||
| char * | sign | ||
| ) |
Converts degrees minutes seconds to radians.
| double | deg, min, sec |
| char | sign : N,E,S,W,-,+ |
Definition at line 692 of file geoPoint.c.
References DEG_TO_RAD, MIN_TO_DEG, and SEC_TO_DEG.
| double geoEfg2Hgt | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 125 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh().
| double geoEfg2Hgt_aa | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 531 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_aa().

| double geoEfg2Hgt_aa_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 392 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_aa_fast().
| double geoEfg2Hgt_aa_its | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 543 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_aa(), and geoEfg2LlhGetIts().

| double geoEfg2Hgt_borkowski | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 638 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_borkowski().
| double geoEfg2Hgt_borkowski_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 489 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_borkowski_fast().

| double geoEfg2Hgt_bowring | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 429 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_bowring().

| double geoEfg2Hgt_bowring_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 318 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_bowring_fast().
| double geoEfg2Hgt_bowring_its | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 441 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_bowring(), and geoEfg2LlhGetIts().

| double geoEfg2Hgt_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 88 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_fast().

| double geoEfg2Hgt_heikkinen | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 831 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_heikkinen().
| double geoEfg2Hgt_hm | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 213 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_hm().

| double geoEfg2Hgt_hm_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 160 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_hm_fast().
| double geoEfg2Hgt_hm_its | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 225 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_hm(), and geoEfg2LlhGetIts().

| double geoEfg2Hgt_toms | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 930 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_toms().

| double geoEfg2Hgt_torge | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 322 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_torge().

| double geoEfg2Hgt_torge_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 236 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_torge_fast().
| double geoEfg2Hgt_torge_its | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 334 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_torge(), and geoEfg2LlhGetIts().

| double geoEfg2Hgt_vermeille | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 730 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_vermeille().
| double geoEfg2Hgt_vermeille_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 576 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, and geoEfg2Llh_vermeille_fast().

| double geoEfg2Lat | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 102 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh(), and RAD_TO_DEG.
| double geoEfg2Lat_aa | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 508 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_aa(), and RAD_TO_DEG.

| double geoEfg2Lat_aa_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 369 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_aa_fast(), and RAD_TO_DEG.
| double geoEfg2Lat_borkowski | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 615 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_borkowski(), and RAD_TO_DEG.
| double geoEfg2Lat_borkowski_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 466 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_borkowski_fast(), and RAD_TO_DEG.

| double geoEfg2Lat_bowring | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 406 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_bowring(), and RAD_TO_DEG.

| double geoEfg2Lat_bowring_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 295 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_bowring_fast(), and RAD_TO_DEG.
| double geoEfg2Lat_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 65 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_fast(), and RAD_TO_DEG.

| double geoEfg2Lat_heikkinen | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 808 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_heikkinen(), and RAD_TO_DEG.
| double geoEfg2Lat_hm | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 190 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_hm(), and RAD_TO_DEG.

| double geoEfg2Lat_hm_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 137 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_hm_fast(), and RAD_TO_DEG.
| double geoEfg2Lat_toms | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 907 of file geoEfg2Llh.c.
References geoEfg2Llh_toms(), and RAD_TO_DEG.

| double geoEfg2Lat_torge | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 299 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_torge(), and RAD_TO_DEG.

| double geoEfg2Lat_torge_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 213 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_torge_fast(), and RAD_TO_DEG.
| double geoEfg2Lat_vermeille | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 707 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_vermeille(), and RAD_TO_DEG.
| double geoEfg2Lat_vermeille_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 553 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_vermeille_fast(), and RAD_TO_DEG.

| void geoEfg2Llh | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 72 of file geoEfg2Llh.c.
References cube, GEO_E, GEO_F, GEO_G, geoGetEllipsoid(), its, p, and sqr.
Referenced by geoEfg2Hgt(), geoEfg2Lat(), and geoEfg2Lon().

| void geoEfg2Llh_aa | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Astronomical Almanac 2002 Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 468 of file geoEfg2Llh.c.
References GEO_E, GEO_EFG2LLH_MAX_ITS, GEO_F, GEO_G, geoAccuracy, geoGetEllipsoid(), its, n(), p, and sqr.
Referenced by geoEfg2Hgt_aa(), geoEfg2Hgt_aa_its(), geoEfg2Lat_aa(), and geoEfg2Lon_aa().
| void geoEfg2Llh_aa_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Astronomical Almanac 2002 Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 347 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_e2, n(), p, and sqr.
Referenced by geoEfg2Hgt_aa_fast(), geoEfg2Lat_aa_fast(), and geoEfg2Lon_aa_fast().

| void geoEfg2Llh_borkowski | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Borkowski Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 571 of file geoEfg2Llh.c.
References cube, GEO_E, GEO_F, GEO_G, geoGetEllipsoid(), its, p, and sqr.
Referenced by geoEfg2Hgt_borkowski(), geoEfg2Lat_borkowski(), and geoEfg2Lon_borkowski().

| void geoEfg2Llh_borkowski_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Borkowski Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 420 of file geoEfg2Llh_fast.c.
References cube, GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_b, p, and sqr.
Referenced by geoEfg2Hgt_borkowski_fast(), geoEfg2Lat_borkowski_fast(), and geoEfg2Lon_borkowski_fast().
| void geoEfg2Llh_bowring | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Bowring Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 362 of file geoEfg2Llh.c.
References cube, GEO_E, GEO_EFG2LLH_MAX_ITS, GEO_F, GEO_G, geoAccuracy, geoGetEllipsoid(), its, n(), p, and sqr.
Referenced by geoEfg2Hgt_bowring(), geoEfg2Hgt_bowring_its(), geoEfg2Lat_bowring(), and geoEfg2Lon_bowring().
| void geoEfg2Llh_bowring_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Bowring Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 264 of file geoEfg2Llh_fast.c.
References cube, GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_b, GEO_WGS84_e2, GEO_WGS84_ee2, n(), p, and sqr.
Referenced by geoEfg2Hgt_bowring_fast(), geoEfg2Lat_bowring_fast(), and geoEfg2Lon_bowring_fast().

| void geoEfg2Llh_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 40 of file geoEfg2Llh_fast.c.
References cube, GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_b, GEO_WGS84_e2, GEO_WGS84_ee2, p, and sqr.
Referenced by geoEfg2Hgt_fast(), geoEfg2Lat_fast(), and geoEfg2Lon_fast().
| void geoEfg2Llh_fast_packed | ( | const GEO_DATUM * | datum, |
| int | count, | ||
| double | efg_llh[] | ||
| ) |
| void geoEfg2Llh_fast_packed2 | ( | const GEO_DATUM * | datum, |
| int | count, | ||
| double | efg_in[], | ||
| double | llh_out[] | ||
| ) |
| void geoEfg2Llh_heikkinen | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
heikkinen Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 758 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoGetEllipsoid(), its, p, sp, and sqr.
Referenced by geoEfg2Hgt_heikkinen(), geoEfg2Lat_heikkinen(), and geoEfg2Lon_heikkinen().

| void geoEfg2Llh_hm | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Hirvonen & Moritz Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 153 of file geoEfg2Llh.c.
References GEO_E, GEO_EFG2LLH_MAX_ITS, GEO_F, GEO_G, geoAccuracy, geoGetEllipsoid(), its, n(), p, and sqr.
Referenced by geoEfg2Hgt_hm(), geoEfg2Hgt_hm_its(), geoEfg2Lat_hm(), and geoEfg2Lon_hm().
| void geoEfg2Llh_hm_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Hirvonen & Moritz Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 116 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_e2, n(), p, and sqr.
Referenced by geoEfg2Hgt_hm_fast(), geoEfg2Lat_hm_fast(), and geoEfg2Lon_hm_fast().

| void geoEfg2Llh_packed | ( | const GEO_DATUM * | datum, |
| int | count, | ||
| double | efg_llh[] | ||
| ) |
| void geoEfg2Llh_toms | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Definition at line 860 of file geoEfg2Llh.c.
References aDc, cube, GEO_E, GEO_F, GEO_G, geoGetEllipsoid(), its, n(), and sqr.
Referenced by geoEfg2Hgt_toms(), geoEfg2Lat_toms(), and geoEfg2Lon_toms().
| void geoEfg2Llh_torge | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Torge Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 253 of file geoEfg2Llh.c.
References GEO_E, GEO_EFG2LLH_MAX_ITS, GEO_F, GEO_G, geoAccuracy, geoGetEllipsoid(), its, n(), p, and sqr.
Referenced by geoEfg2Hgt_torge(), geoEfg2Hgt_torge_its(), geoEfg2Lat_torge(), and geoEfg2Lon_torge().
| void geoEfg2Llh_torge_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Torge Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 188 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_e2, n(), p, and sqr.
Referenced by geoEfg2Hgt_torge_fast(), geoEfg2Lat_torge_fast(), and geoEfg2Lon_torge_fast().

| void geoEfg2Llh_vermeille | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Vermeille Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 666 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoGetEllipsoid(), its, k, p, and sqr.
Referenced by geoEfg2Hgt_vermeille(), geoEfg2Lat_vermeille(), and geoEfg2Lon_vermeille().

| void geoEfg2Llh_vermeille_fast | ( | int | datum, |
| double | efg[], | ||
| double * | lat, | ||
| double * | lon, | ||
| double * | hgt | ||
| ) |
Vermeille Method - This routine will convert earth centered Cartesian coordinates (E,F,G), into geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ).
).
| int | datum |
| double | efg[] : EFG(xyz) in METERS |
| double | *lat : Latitude in RADIANS |
| double | *lon : Longitude in RADIANS |
| double | *hgt : Height in METERS |
Definition at line 517 of file geoEfg2Llh_fast.c.
References cube, GEO_E, GEO_F, GEO_G, GEO_WGS84_a, GEO_WGS84_e2, k, p, and sqr.
Referenced by geoEfg2Hgt_vermeille_fast(), geoEfg2Lat_vermeille_fast(), and geoEfg2Lon_vermeille_fast().
| int geoEfg2LlhGetIts | ( | void | ) |
Definition at line 25 of file geoEfg2Llh.c.
References its.
Referenced by geoEfg2Hgt_aa_its(), geoEfg2Hgt_bowring_its(), geoEfg2Hgt_hm_its(), and geoEfg2Hgt_torge_its().
| double geoEfg2Lon | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 114 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh(), and RAD_TO_DEG.
| double geoEfg2Lon_aa | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 520 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_aa(), and RAD_TO_DEG.

| double geoEfg2Lon_aa_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 381 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_aa_fast(), and RAD_TO_DEG.
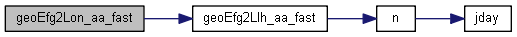
| double geoEfg2Lon_borkowski | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 627 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_borkowski(), and RAD_TO_DEG.
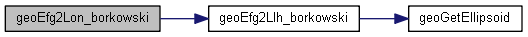
| double geoEfg2Lon_borkowski_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 478 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_borkowski_fast(), and RAD_TO_DEG.

| double geoEfg2Lon_bowring | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 418 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_bowring(), and RAD_TO_DEG.

| double geoEfg2Lon_bowring_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 307 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_bowring_fast(), and RAD_TO_DEG.
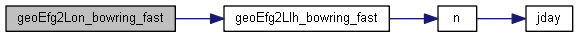
| double geoEfg2Lon_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 77 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_fast(), and RAD_TO_DEG.

| double geoEfg2Lon_heikkinen | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 820 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_heikkinen(), and RAD_TO_DEG.
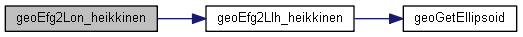
| double geoEfg2Lon_hm | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 202 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_hm(), and RAD_TO_DEG.

| double geoEfg2Lon_hm_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 149 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_hm_fast(), and RAD_TO_DEG.
| double geoEfg2Lon_toms | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 919 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_toms(), and RAD_TO_DEG.

| double geoEfg2Lon_torge | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 311 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_torge(), and RAD_TO_DEG.

| double geoEfg2Lon_torge_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 225 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_torge_fast(), and RAD_TO_DEG.
| double geoEfg2Lon_vermeille | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 719 of file geoEfg2Llh.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_vermeille(), and RAD_TO_DEG.
| double geoEfg2Lon_vermeille_fast | ( | int | datum, |
| double | e, | ||
| double | f, | ||
| double | g | ||
| ) |
Definition at line 565 of file geoEfg2Llh_fast.c.
References GEO_E, GEO_F, GEO_G, geoEfg2Llh_vermeille_fast(), and RAD_TO_DEG.

| int geoEfg2XyzDiff | ( | GEO_LOCATION * | src_desc, |
| GEO_LOCATION * | tgt_desc, | ||
| double | xyz_disp[] | ||
| ) |
This function returns the XYZ offset of the target point with respect to the source point, given the Earth Fixed Geodetic coordinates of the points. The EFG coordinates for the source must appear in the GEO_LOCATION record, which must be built previous to the call to this procedure.
| GEO_LOCATION | *src_desc |
| GEO_LOCATION | *tgt_desc |
| double | xyz_disp[] |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 50 of file geoPoint.c.
References GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::e, GEO_LOCATION::f, GEO_LOCATION::g, GEO_OK, GEO_X, GEO_Y, GEO_Z, GEO_LOCATION::slat, and GEO_LOCATION::slon.
Referenced by geoLlh2DiffX(), geoLlh2DiffY(), and geoLlh2DiffZ().
| int geoEfg2XyzDiff_packed | ( | GEO_LOCATION * | src_desc, |
| int | count, | ||
| double | efg_xyz[] | ||
| ) |
This function returns the XYZ offset of the target point with respect to the source point, given the Earth Fixed Geodetic coordinates of the points. The EFG coordinates for the source must appear in the GEO_LOCATION record, which must be built previous to the call to this procedure.
| GEO_LOCATION | *src_desc |
| GEO_LOCATION | *tgt_desc |
| double | xyz_disp[] |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 96 of file geoPoint.c.
References GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::e, GEO_LOCATION::f, GEO_LOCATION::g, GEO_E, GEO_F, GEO_G, GEO_OK, GEO_X, GEO_Y, GEO_Z, GEO_LOCATION::slat, and GEO_LOCATION::slon.
| void geoGetEllipsoid | ( | double * | a, |
| double * | b, | ||
| double * | e2, | ||
| double * | ee2, | ||
| double * | f, | ||
| int | datum | ||
| ) |
This routine computes essential datum values from basic parameters obtained from the ellips structure.
| double | *a : Major axis ( Meters ) |
| double | *b : Minor axis ( Meters ) |
| double | *e2 : Eccentricity |
| double | *ee2 : Eccentricity prime |
| double | *f : Flattening |
| int | datum : Datum to use |
Definition at line 189 of file geoEllips.c.
References GEO_ELLIPSOID::a, GEO_B, GEO_E2, GEO_E2P, and GEO_FL.
Referenced by geoEfg2Llh(), geoEfg2Llh_aa(), geoEfg2Llh_borkowski(), geoEfg2Llh_bowring(), geoEfg2Llh_heikkinen(), geoEfg2Llh_hm(), geoEfg2Llh_toms(), geoEfg2Llh_torge(), geoEfg2Llh_vermeille(), geoInitLocation(), and geoLlh2Efg().
| int geoGetSunError | ( | void | ) |
Definition at line 198 of file geoAstro.c.
References geoSunError.
| int geoGettm | ( | int | part) |
| int geoInitDatum | ( | GEO_DATUM * | d, |
| int | datum | ||
| ) |
| int geoInitLocation | ( | GEO_LOCATION * | l, |
| double | lat, | ||
| double | lon, | ||
| double | hgt, | ||
| int | datum, | ||
| char * | name | ||
| ) |
This routine needs to be called when a site (or location) is initialized. Several of the routines use the information in the structure that this routine fills.
| GEO_LOCATION | *l |
| double | lat |
| double | lon |
| double | hgt |
| int | datum |
| char | *name //Name of the site location |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 96 of file geoEllips.c.
References GEO_DATUM::a, GEO_DATUM::b, GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::clonclat, GEO_LOCATION::clonslat, GEO_LOCATION::datum, GEO_DATUM::datum_num, DEG_TO_RAD, GEO_LOCATION::e, GEO_DATUM::e2, GEO_DATUM::ee2, GEO_LOCATION::efg, GEO_LOCATION::f, GEO_DATUM::flat, GEO_LOCATION::g, GEO_DATUM_MAX, GEO_E, GEO_ERROR, GEO_F, GEO_G, GEO_OK, geoGetEllipsoid(), geoMagFillDec(), GEO_LOCATION::hgt, GEO_LOCATION::lat, GEO_LOCATION::lon, GEO_DATUM::m1e2, GEO_LOCATION::name, GEO_LOCATION::rlat, GEO_LOCATION::rlon, GEO_LOCATION::slat, GEO_LOCATION::slon, GEO_LOCATION::slonclat, GEO_LOCATION::slonslat, GEO_LOCATION::timezone, and GEO_LOCATION::tlat.
Referenced by geoLlh2DiffX(), geoLlh2DiffY(), geoLlh2DiffZ(), geoLlh2E(), geoLlh2F(), geoLlh2G(), geoSunNowAz(), and geoSunNowEl().

| int geoInitLocation2 | ( | GEO_LOCATION * | l, |
| double | lat, | ||
| double | lon, | ||
| double | hgt, | ||
| const GEO_DATUM * | datum, | ||
| const char * | name | ||
| ) |
| double geoLlh2DiffX | ( | double | lat1, |
| double | lon1, | ||
| double | hgt1, | ||
| int | datum1, | ||
| double | lat2, | ||
| double | lon2, | ||
| double | hgt2, | ||
| int | datum2 | ||
| ) |
Definition at line 130 of file geoPoint.c.
References GEO_X, geoEfg2XyzDiff(), and geoInitLocation().

| double geoLlh2DiffY | ( | double | lat1, |
| double | lon1, | ||
| double | hgt1, | ||
| int | datum1, | ||
| double | lat2, | ||
| double | lon2, | ||
| double | hgt2, | ||
| int | datum2 | ||
| ) |
Definition at line 142 of file geoPoint.c.
References GEO_Y, geoEfg2XyzDiff(), and geoInitLocation().

| double geoLlh2DiffZ | ( | double | lat1, |
| double | lon1, | ||
| double | hgt1, | ||
| int | datum1, | ||
| double | lat2, | ||
| double | lon2, | ||
| double | hgt2, | ||
| int | datum2 | ||
| ) |
Definition at line 153 of file geoPoint.c.
References GEO_Z, geoEfg2XyzDiff(), and geoInitLocation().

| double geoLlh2E | ( | double | lat, |
| double | lon, | ||
| double | hgt, | ||
| int | datum | ||
| ) |
This routine will convert geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the E component.
) into earth centered Cartesian coordinates (E,F,G). This returns the E component.
| double | lat : Latitude in RADIANS |
| double | lon : Longitude in RADIANS |
| double | height : Height in METERS |
| int | datum1 |
Definition at line 262 of file geoPoint.c.
References GEO_LOCATION::e, and geoInitLocation().

| void geoLlh2Efg | ( | double | lat, |
| double | lon, | ||
| double | height, | ||
| int | datum, | ||
| double * | e, | ||
| double * | f, | ||
| double * | g | ||
| ) |
This routine will convert geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G).
) into earth centered Cartesian coordinates (E,F,G).
| double | lat : Latitude in RADIANS |
| double | lon : Longitude in RADIANS |
| double | height : Height in METERS |
| int | datum1 |
| double | *e : E(x) in METERS |
| double | *f : F(y) in METERS |
| double | *g : G(z) in METERS |
Definition at line 181 of file geoPoint.c.
References geoGetEllipsoid().

| void geoLlh2Efg_packed | ( | GEO_DATUM * | datum, |
| int | count, | ||
| double | llh_efg[] | ||
| ) |
This routine will convert geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G).
) into earth centered Cartesian coordinates (E,F,G).
| GEO_DATUM* | datum Datum of the lat/lon/height |
| int | count Number of vertices |
| double | llh_efg[] Pointer to the first coordinate of the first vertex of the array. |
Definition at line 214 of file geoPoint.c.
References GEO_DATUM::a, GEO_DATUM::e2, GEO_E, GEO_F, GEO_G, GEO_HGT, GEO_LAT, and GEO_LON.
| double geoLlh2F | ( | double | lat, |
| double | lon, | ||
| double | hgt, | ||
| int | datum | ||
| ) |
This routine will convert geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the F component.
) into earth centered Cartesian coordinates (E,F,G). This returns the F component.
| double | lat : Latitude in RADIANS |
| double | lon : Longitude in RADIANS |
| double | height : Height in METERS |
| int | datum1 |
Definition at line 286 of file geoPoint.c.
References GEO_LOCATION::f, and geoInitLocation().

| double geoLlh2G | ( | double | lat, |
| double | lon, | ||
| double | hgt, | ||
| int | datum | ||
| ) |
This routine will convert geodetic coordinates (latitude  , longitude
, longitude  , and ellipsoid height
, and ellipsoid height  ) into earth centered Cartesian coordinates (E,F,G). This returns the G component.
) into earth centered Cartesian coordinates (E,F,G). This returns the G component.
| double | lat : Latitude in RADIANS |
| double | lon : Longitude in RADIANS |
| double | height : Height in METERS |
| int | datum1 |
Definition at line 310 of file geoPoint.c.
References GEO_LOCATION::g, and geoInitLocation().

| int geoMag | ( | double | alt, |
| double | glat, | ||
| double | glon, | ||
| double | time, | ||
| double * | dec, | ||
| double * | dip, | ||
| double * | ti, | ||
| double * | gv, | ||
| double * | adec, | ||
| double * | adip, | ||
| double * | ati, | ||
| double * | x, | ||
| double * | y, | ||
| double * | z, | ||
| double * | h, | ||
| double * | ax, | ||
| double * | ay, | ||
| double * | az, | ||
| double * | ah | ||
| ) |
This routine computes all of the relevant geomagnetic data.
| double | alt : in: altitude in meters |
| double | glat : in: latitude in decimal degrees |
| double | glon : in: longitude in decimal degrees |
| double | time : in: time in decimal years |
| double | *dec :out: declination in degrees |
| double | *dip :out: dip in degrees |
| double | *ti :out: total intensity in nT |
| double | *gv :out: geomagnetic grid variation |
| double | *adec :out: Annual declination in degrees |
| double | *adip :out: Annual dip in degrees |
| double | *ati :out: Annual total intensity in nT |
| double | *x :out: X Component of the magnetic field |
| double | *y :out: Y Component of the magnetic field |
| double | *z :out: Z Component of the magnetic field |
| double | *h :out: h Component of the magnetic field |
| double | *ax :out: Annual X Component of the magnetic field |
| double | *ay :out: Annual Y Component of the magnetic field |
| double | *az :out: Annual Z Component of the magnetic field |
| double | *ah :out: Annual H Component of the magnetic field |
| GEO_OK | on success |
| GEO_ERROR | on error |
{
Definition at line 523 of file geoMag.c.
References DEG_TO_MIN, DEG_TO_RAD, GEO_OK, geoMagInit(), and geomg1().
| int geoMagFillDec | ( | GEO_LOCATION * | l, |
| double * | dec | ||
| ) |
Definition at line 903 of file geoMag.c.
References GEO_LOCATION::Declination, GEO_OK, geoMagGetDec(), GEO_LOCATION::hgt, GEO_LOCATION::lat, and GEO_LOCATION::lon.
Referenced by geoInitLocation().

| int geoMagGetDec | ( | double | lat, |
| double | lon, | ||
| double | hgt, | ||
| int | month, | ||
| int | day, | ||
| int | year, | ||
| double * | dec | ||
| ) |
This routine computes magnetic declination.
| double | lat : in: latitude in decimal degrees |
| double | lon : in: longitude in decimal degrees |
| double | hgt : in: altitude in meters |
| int | month : in: Month of the year |
| int | day : in: Day of the month |
| int | year : in: Year |
| double | dec :out: declination in degrees |
Definition at line 825 of file geoMag.c.
References GEO_OK, geoMagInit(), geomg1(), and jday().
Referenced by geoMagFillDec(), and geoMagGetDecNow().
| double geoMagGetDecNow | ( | double | lat, |
| double | lon, | ||
| double | hgt | ||
| ) |
This routine computes magnetic declination for now time.
| double | lat : in: latitude in decimal degrees |
| double | lon : in: longitude in decimal degrees |
| double | hgt : in: altitude in meters |
| double | dec :out: declination in degrees |
Definition at line 882 of file geoMag.c.
References geoMagGetDec().

| double geoMagGetDecRet | ( | double | lat, |
| double | lon, | ||
| double | hgt, | ||
| int | month, | ||
| int | day, | ||
| int | year | ||
| ) |
This routine computes and returns magnetic declination for a specific date.
| double | lat : in: latitude in decimal degrees |
| double | lon : in: longitude in decimal degrees |
| double | hgt : in: altitude in meters |
| int | month : in: Month of the year |
| int | day : in: Day of the month |
| int | year : in: Year |
| double | dec :out: declination in degrees |
Definition at line 855 of file geoMag.c.
References geoMagInit(), geomg1(), and jday().
| int geomg1 | ( | double | alt, |
| double | glat, | ||
| double | glon, | ||
| double | time, | ||
| double * | dec, | ||
| double * | dip, | ||
| double * | ti, | ||
| double * | gv | ||
| ) |
This is documentation that came with the WMM. It is included here for completeness.
// MAXDEG - MAXIMUM DEGREE OF SPHERICAL HARMONIC MODEL (INPUT) // TIME - COMPUTATION TIME (YRS) (INPUT) // (EG. 1 JULY 1995 = 1995.500) // ALT - GEODETIC ALTITUDE (M) (INPUT) // GLAT - GEODETIC LATITUDE (DEG.) (INPUT) // GLON - GEODETIC LONGITUDE (DEG.) (INPUT) // EPOCH - BASE TIME OF GEOMAGNETIC MODEL (YRS) // P(N,M) - ASSOCIATED LEGENDRE POLYNOMIALS (UNNORMALIZED) // DEC - GEOMAGNETIC DECLINATION (DEG.) (OUTPUT) // EAST=POSITIVE ANGLES // WEST=NEGATIVE ANGLES // DIP - GEOMAGNETIC INCLINATION (DEG.) (OUTPUT) // DOWN=POSITIVE ANGLES // UP=NEGATIVE ANGLES // TI - GEOMAGNETIC TOTAL INTENSITY (NT) (OUTPUT) // GV - GEOMAGNETIC GRID VARIATION (DEG.) (OUTPUT) // REFERENCED TO GRID NORTH // GRID NORTH REFERENCED TO 0 MERIDIAN // OF A POLAR STEREOGRAPHIC PROJECTION // (ARCTIC/ANTARCTIC ONLY) // A - SEMIMAJOR AXIS OF WGS-84 ELLIPSOID (KM) // B - SEMIMINOR AXIS OF WGS-84 ELLIPSOID (KM) // RE - MEAN RADIUS OF IAU-66 ELLIPSOID (KM) // a2, // a * a // b2, // b * b // c2, // a2 - b2 // a4, // a2 * a2 // b4, // b2 * b2 // c4, // a4 - b4 // ct, //C CT - COSINE OF (SPHERICAL COORD. LATITUDE) // st, //C ST - SINE OF (SPHERICAL COORD. LATITUDE) // r2, // r, //C R - SPHERICAL COORDINATE RADIAL POSITION (KM) // ca, //C CA - COSINE OF SPHERICAL TO GEODETIC VECTOR ROTATION ANGLE // sa, //C SA - SINE OF SPHERICAL TO GEODETIC VECTOR ROTATION ANGLE // br, //C BR - RADIAL COMPONENT OF GEOMAGNETIC FIELD (NT) // bt, //C BT - THETA COMPONENT OF GEOMAGNETIC FIELD (NT) // bp, //C BP - PHI COMPONENT OF GEOMAGNETIC FIELD (NT) // bx, //C BX - NORTH GEOMAGNETIC COMPONENT (NT) // by, //C BY - EAST GEOMAGNETIC COMPONENT (NT) // bz, //C BZ - VERTICALLY DOWN GEOMAGNETIC COMPONENT (NT) // bh; //C BH - HORIZONTAL GEOMAGNETIC COMPONENT (NT)
Definition at line 595 of file geoMag.c.
References GEO_ELLIPSOID::a, c, cd, CIRCLE, cp, DEG_TO_RAD, dp, ellips, epoch, fm, fn, GEO_B, GEO_DATUM_WE, GEO_OK, HALF_CIRCLE, k, maxord, n(), p, pp, RAD_TO_DEG, sp, and tc.
Referenced by geoMag(), geoMagGetDec(), and geoMagGetDecRet().

| double geoRads2DD | ( | double | rads) |
Converts radians to Decimal Degrees.
| double | radians |
Definition at line 836 of file geoPoint.c.
References RAD_TO_DEG.
| double geoRads2Decdms | ( | double | rads) |
Convert radians to decimal degrees, minutes, and seconds ("dddmmss.s").
| double | rads |
Definition at line 810 of file geoPoint.c.
References RAD_TO_DEG.
| void geoRads2Dms | ( | double | rads, |
| double * | deg, | ||
| double * | min, | ||
| double * | sec, | ||
| double * | dir | ||
| ) |
Converts radians to degrees minutes seconds.
| double | rads |
| double | deg, min, sec |
| char | dir : -1.0 or 1.0 |
Definition at line 782 of file geoPoint.c.
References RAD_TO_DEG.
| void geoRae2Efg | ( | GEO_LOCATION * | loc, |
| double | aer_in[], | ||
| double | efg_out[] | ||
| ) |
Ingests Range, Azimuth, Elevation and site info and returns the EFG coordinates that the RAE points to.
| GEO_LOCATION | *loc |
| double | aer_in[] |
| double | efg_out[] |
Definition at line 654 of file geoPoint.c.
References GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::e, GEO_LOCATION::f, GEO_LOCATION::g, GEO_E, GEO_F, GEO_G, GEO_X, GEO_Y, GEO_Z, geoRae2Xyz(), GEO_LOCATION::slat, and GEO_LOCATION::slon.

| void geoRae2Xyz | ( | double | rae_in[], |
| double | xyz_out[] | ||
| ) |
This routine converts from Range, Azimuth, and Elevation into Cartesian coordinates X,Y,Z.
| double | rae_in[] |
| double | xyz_out[] |
Definition at line 501 of file geoPoint.c.
References GEO_AZ, GEO_EL, GEO_RNG, GEO_X, GEO_Y, and GEO_Z.
Referenced by geoRae2Efg().
| void geoRae2Xyz_packed | ( | int | count, |
| double | rae_xyz[] | ||
| ) |
This routine iterates over count vertices in the array rae_xyz converting it from Range, Azimuth, and Elevation into Cartesian coordinates X,Y,Z.
| count | Number of vertices |
| rae_xyz[] | Pointer to the first coordinate of the first vertex of the array. |
Definition at line 522 of file geoPoint.c.
References GEO_AZ, GEO_EL, GEO_RNG, GEO_X, GEO_Y, and GEO_Z.
| int geoSetAccuracy | ( | double | acc) |
This routine will set the accuracy of the iterative Efg2Llh routines (geoEfg2Llh_hm, geoEfg2Llh_torge, geoEfg2Llh_bowring, geoEfg2Llh_aa)
| double | acc : Accuracy in degrees |
| GEO_OK | on success |
| GEO_ERROR | on error |
Several definitions may be used with this function: GEO_EFG2LLH_ACCURACY_METER = 0.00001 degrees GEO_EFG2LLH_ACCURACY_CM = 0.0000001 degrees GEO_EFG2LLH_ACCURACY_MM = 0.00000001 degrees
Definition at line 45 of file geoEfg2Llh.c.
References GEO_ERROR, GEO_OK, and geoAccuracy.
| void geoSetTimeZone | ( | GEO_LOCATION * | l, |
| double | tz, | ||
| int | dst | ||
| ) |
Definition at line 169 of file geoEllips.c.
References GEO_LOCATION::dst, and GEO_LOCATION::timezone.
| int geoSun | ( | GEO_LOCATION * | loc, |
| struct tm * | newtime, | ||
| double * | az, | ||
| double * | el | ||
| ) |
Definition at line 98 of file geoSun.c.
References GEO_LOCATION::clat, DEG_TO_RAD, fractionalYearRad(), GEO_OK, GEO_LOCATION::lon, RAD_TO_DEG, GEO_LOCATION::slat, and GEO_LOCATION::timezone.
Referenced by geoSunPosition().

| int geoSunAA | ( | GEO_LOCATION * | loc, |
| struct tm * | newtime, | ||
| double * | az, | ||
| double * | el | ||
| ) |
Definition at line 482 of file geoSun.c.
References c, DEG_TO_RAD, JD(), obliquity(), RAD_TO_DEG, and GEO_LOCATION::timezone.
| int geoSunAzElJD | ( | GEO_LOCATION * | loc, |
| double * | az, | ||
| double * | el, | ||
| double | tjd_now | ||
| ) |
This routine uses a previously determined Julian date and then gets the Az and El of the sun at this location based on the Julian date.
| GEO_LOCATION | *loc : Location structure |
| double | *az : Azimuth in decimal degrees |
| double | *el : Elevation in decimal degrees |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 147 of file geoAstro.c.
References BODY_SUN, GEO_ERROR, GEO_OK, geoSunError, GEO_LOCATION::hgt, GEO_LOCATION::lat, GEO_LOCATION::lon, MAJOR_PLANET, and REDUCED_ACC.
Referenced by geoSunAzEltm().
| int geoSunAzElNow | ( | GEO_LOCATION * | loc, |
| double * | az, | ||
| double * | el | ||
| ) |
this routine uses ANSI C time routines to obtain the current time and then get the az and el of the sun at this location
| GEO_LOCATION | *loc : Location structure |
| double | *az : Azimuth in decimal degrees |
| double | *el : Elevation in decimal degrees |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 31 of file geoAstro.c.
References geoSunAzEltm().
Referenced by geoSunNowAz(), and geoSunNowEl().

| int geoSunAzEltm | ( | GEO_LOCATION * | loc, |
| double * | az, | ||
| double * | el, | ||
| struct tm * | newtime | ||
| ) |
this routine ingests an ANSI C time structure and then gets the az and el of the sun at this location based on this time.
| GEO_LOCATION | *loc : Location structure |
| double | *az : Azimuth in decimal degrees |
| double | *el : Elevation in decimal degrees |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 98 of file geoAstro.c.
References geoSunAzElJD(), and tError.
Referenced by geoSunAzElNow().

| int geoSunM | ( | GEO_LOCATION * | loc, |
| struct tm * | newtime, | ||
| double * | az, | ||
| double * | el | ||
| ) |
Definition at line 158 of file geoSun.c.
References GEO_LOCATION::clat, DEG_TO_RAD, GEO_LOCATION::dst, GEO_OK, JD(), jday(), GEO_LOCATION::lon, M_PI, RAD_TO_DEG, GEO_LOCATION::slat, GEO_LOCATION::timezone, and TWO_PI.
| double geoSunNowAz | ( | double | lat, |
| double | lon, | ||
| double | hgt | ||
| ) |
this routine uses the location and current time to get the azimuth of the sun at this location
| double | lat : Latitude in degrees |
| double | lon : Longitude in degrees |
| double | hgt : Height in meters |
| double | : Azimuth in decimal degrees |
Definition at line 75 of file geoAstro.c.
References GEO_DATUM_DEFAULT, geoInitLocation(), and geoSunAzElNow().

| double geoSunNowEl | ( | double | lat, |
| double | lon, | ||
| double | hgt | ||
| ) |
this routine uses the location and current time to get the elevation of the sun at this location
| double | lat : Latitude in degrees |
| double | lon : Longitude in degrees |
| double | hgt : Height in meters |
| double | : Elevation in decimal degrees |
Definition at line 54 of file geoAstro.c.
References GEO_DATUM_DEFAULT, geoInitLocation(), and geoSunAzElNow().

| int geoSunPosition | ( | GEO_LOCATION * | loc, |
| double * | az, | ||
| double * | el | ||
| ) |
this routine uses ANSI C time routines to obtain the current time and then get the az and el of the sun at this location
| GEO_LOCATION | *loc : Location structure |
| double | *az : Azimuth in decimal degrees |
| double | *el : Elevation in decimal degrees |
| GEO_OK | on success |
| GEO_ERROR | on error |
Definition at line 84 of file geoSun.c.
References GEO_OK, and geoSun().

| double geoVersion | ( | void | ) |
This function returns the version of the GeoStarsLib.
| GEOSTARSLIB_VERSION | as a double |
Definition at line 25 of file geoPoint.c.
References GEOSTARSLIB_VERSION.
| double geoXyz2A | ( | double | x, |
| double | y, | ||
| double | z | ||
| ) |
Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the azimuth to that point.
Notes:
| double | xyz_in[] |
Definition at line 455 of file geoPoint.c.
References GEO_AZ, geoXyz2Rae(), and RAD_TO_DEG.

| double geoXyz2E | ( | double | x, |
| double | y, | ||
| double | z | ||
| ) |
Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the elevation angle to that point.
Notes:
| double | xyz_in[] |
Definition at line 482 of file geoPoint.c.
References GEO_EL, geoXyz2Rae(), and RAD_TO_DEG.

| void geoXyz2Efg | ( | GEO_LOCATION * | loc, |
| double | xyz_in[], | ||
| double | efg_out[] | ||
| ) |
Ingests X, Y, Z, and site info and returns the EFG coordinates.
| GEO_LOCATION | *loc |
| double | xyz_in[] |
| double | efg_out[] |
Definition at line 570 of file geoPoint.c.
References GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::e, GEO_LOCATION::f, GEO_LOCATION::g, GEO_E, GEO_F, GEO_G, GEO_X, GEO_Y, GEO_Z, GEO_LOCATION::slat, and GEO_LOCATION::slon.
| void geoXyz2Efg_packed | ( | GEO_LOCATION * | loc, |
| int | count, | ||
| double | xyz_efg[] | ||
| ) |
This routine takes site info and iterates over count vertices in the tightly packed array xyz_efg converting it from cartesian XYZ into geocentric EFG coordinates.
| loc | The location that the XYZ grid is based around |
| count | The number of vertices in the array |
| xyz_efg[] | Pointer to the first vertex of the array |
Definition at line 606 of file geoPoint.c.
References GEO_LOCATION::clat, GEO_LOCATION::clon, GEO_LOCATION::e, GEO_LOCATION::f, GEO_LOCATION::g, GEO_E, GEO_F, GEO_G, GEO_X, GEO_Y, GEO_Z, GEO_LOCATION::slat, and GEO_LOCATION::slon.
| double geoXyz2R | ( | double | x, |
| double | y, | ||
| double | z | ||
| ) |
Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2R calculates the range to that point.
Notes:
| double | xyz_in[] |
Definition at line 428 of file geoPoint.c.
References GEO_RNG, and geoXyz2Rae().

| void geoXyz2Rae | ( | double | xyz_in[], |
| double | rae_out[] | ||
| ) |
Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2Rae calculates the range, azimuth, and elevation to that point.
Notes:
| double | xyz_in[] |
| double | rae_out[] |
Definition at line 339 of file geoPoint.c.
References GEO_AZ, GEO_EL, GEO_RNG, GEO_X, GEO_Y, GEO_Z, and M_PI.
Referenced by geoXyz2A(), geoXyz2E(), and geoXyz2R().
| void geoXyz2Rae_packed | ( | int | count, |
| double | xyz_rae[] | ||
| ) |
Given the X, Y, and Z coordinates (in meters) of a point in space, the procedure geoXyz2Rae calculates the range, azimuth, and elevation to that point.
Notes:
| count | Number of vertices |
| xyz_rae[] | Pointer to the first coordinate of the first vertex of the array. |
Definition at line 378 of file geoPoint.c.
References GEO_AZ, GEO_EL, GEO_RNG, GEO_X, GEO_Y, GEO_Z, and M_PI.
| GEO_ELLIPSOID ellips[] |
This structure array contains the all of the ellipsoids used in this library.
Definition at line 46 of file geoEllips.c.
Referenced by geomg1().
| double geoAccuracy |
Definition at line 21 of file geoEfg2Llh.c.
Referenced by geoEfg2Llh_aa(), geoEfg2Llh_bowring(), geoEfg2Llh_hm(), geoEfg2Llh_torge(), and geoSetAccuracy().
| int geoSunError |
Definition at line 15 of file geoAstro.c.
Referenced by geoGetSunError(), and geoSunAzElJD().
 1.8.4
1.8.4