 |
Geo Stars Library
0.9.3
Geodetic and Astrometry library
|
 |
Geo Stars Library
0.9.3
Geodetic and Astrometry library
|
Geodetic Library routines augmented by astrometry routines
Table of Contents
This geodetic library has functions for dealing with many geodesy-based problems found in positioning, pointing, and surveying situations. It is useful to determine absolute position on the earth, pointing vectors, coordinate transformations, and deg/min/sec conversions. It has the following features:
Geo Library was designed to be as flexible as possible. It does not come as a linkable library. You compile the code on your command line or place it in your own library. Geo Library contains these files:
Test Code
Novas could be located in a subdirectory called novas in the main code tree. When using Novas, you will need to compile in the following files:
There are also header files in that directory that you may want to make your compiler aware of. Novas source code is not supplied with GeoStars Library. It can be downloaded from http://aa.usno.navy.mil/software/novas/novas_info.html
Example compilation with GNU C++
with novas already in a library:
with Novas not in a library:
Example compilation with Borland C++
with novas already in a library:
with Novas not in a library:
Example compilation with Microsoft C++
with novas already in a library:
with Novas not in a library:
Calling the geo.dll from Visual Basic
Example:
More examples and definintions are included in geo.bas and geoTest.bas.
\ref HomeEllipsoids
Contrary to popular belief, the Earth is not round. It, like most people, is a bit bigger around the girth. That girth is called the equator. The equator is one of the two axis of the Earth. The other axis is the polar axis.
Ellipsoids contain several defining values:
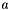

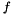 is represented by
is represented by
![\[f = \frac{a - b}{a}\]](form_6.png)
 ). Inverse Flattening
). Inverse Flattening 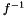 is, of course, the denominator of the fraction.
is, of course, the denominator of the fraction. 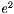 is represented by
is represented by
![\[e^2 = \frac{a^2 - b^2}{a^2}\]](form_10.png)
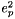 is represented by
is represented by
![\[e^2_p = \frac{a^2 - b^2}{b^2}\]](form_12.png)

The Geo Library contains definitions of the following ellipsoids:
Ellipsoid Name, ID, Major Axis, Inverse Flattening
---------------------------------------------------------------------------
Airy 1830, AA, 6377563.396, 299.3249646
Australian National, AN, 6378160.0 , 298.25
Bessel 1841, BR, 6377397.155, 299.1528128
Bessel 1841 (Namibia), BN, 6377483.865, 299.1528128
Clarke 1866, CC, 6378206.4 , 294.9786982
Clarke 1880, CD, 6378249.145, 293.465
Everest (Brunei, E. Malaysia ), EB, 6377298.556, 300.8017
Everest 1830, EA, 6377276.345, 300.8017
Everest 1956 (India and Nepal), EC, 6377301.243, 300.8017
Everest (Pakistan), EF, 6377309.613, 300.8017
Everest 1948 (W. Malaysia and Singapore), EE, 6377304.063, 300.8017
Everest 1969 (W. Malaysia), ED, 6377295.664, 300.8017
Geodetic Reference System 1980, RF, 6378137.0 , 298.257222101
Helmert 1906, HE, 6378200.0 , 298.3
Hough 1960, HO, 6378270.0 , 297.0
Indonesian 1974, ID, 6378160.0 , 298.247
International 1924, IN, 6378388.0 , 297.0
Krassovsky 1940, KA, 6378245.0 , 298.3
Modified Airy, AM, 6377340.189, 299.3249646
Modified Fischer 1960, FA, 6378155.0 , 298.3
South American 1969, SA, 6378160.0 , 298.25
WGS 1972, WD, 6378135.0 , 298.26
WGS 1984, WE, 6378137.0 , 298.257223563
NAD 1983, 83, 6378137.0 ,298.257222101
\ref Home
There are several coordinate systems used in the Geo Library.
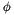 ), Longitude (
), Longitude ( 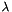 ), Height (
), Height (  ) This coordinate system references a point on the Earth's ellipsoid. Latitude and longitude are measured in degrees. Height is measured in meters.
) This coordinate system references a point on the Earth's ellipsoid. Latitude and longitude are measured in degrees. Height is measured in meters.
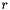 ), Azimuth (
), Azimuth ( 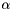 ), Elevation (
), Elevation ( 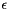 ) This polar coordinate system originates from a point on the Earth's ellipsoid. Range (
) This polar coordinate system originates from a point on the Earth's ellipsoid. Range ( 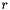 ) is measured in meters and represents the slant range from the origin to the point. Azimuth (
) is measured in meters and represents the slant range from the origin to the point. Azimuth ( 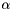 ) is measured clockwise from north (zero degrees) in degrees.
) is measured clockwise from north (zero degrees) in degrees. 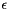 is measured from the tangential plane upward. Also in degrees.
is measured from the tangential plane upward. Also in degrees.

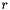 , Azimuth
, Azimuth 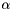 , and Elevation
, and Elevation 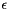 to X,Y,Z If the slant range
to X,Y,Z If the slant range 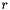 , azimuth
, azimuth 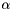 , and elevation
, and elevation 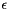 from the origin to a point are known, topocentric Cartesian coordinates can be computed in the following manner:
from the origin to a point are known, topocentric Cartesian coordinates can be computed in the following manner:


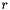 , Azimuth
, Azimuth 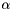 , and Elevation
, and Elevation 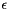 If Cartesian coordinates X,Y,Z are known, then slant range
If Cartesian coordinates X,Y,Z are known, then slant range 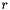 , azimuth
, azimuth 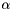 , and elevation
, and elevation 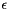 can be determined this way:
can be determined this way:
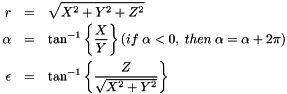
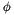 , Longitude
, Longitude 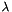 , Height
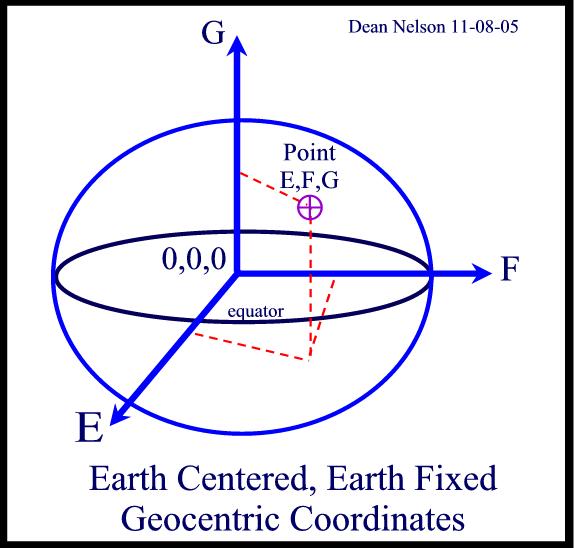
, Height  to E,F,G Geodetic coordinates, Latitude, longitude, and height can be converted to geocentric coordinates through this method:
to E,F,G Geodetic coordinates, Latitude, longitude, and height can be converted to geocentric coordinates through this method:
![\begin{eqnarray*} Radius \; of \; curvature: \; N &=&\frac{a}{\sqrt{1-e^2\sin^2\phi}} \\ E &=& \left(N+h\right) \; \cos\phi \; \cos\lambda \\ F &=& \left(N+h\right) \; \cos\phi \; \sin\lambda \\ G &=& \left[N\left(1-e^2\right)+h\right] \; \sin\phi \\ \end{eqnarray*}](form_18.png)
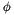 , Longitude
, Longitude 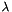 , Height
, Height  Geocentric coordinates E,F,G can be converted to latitude
Geocentric coordinates E,F,G can be converted to latitude 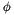 , longitude
, longitude 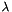 , and height
, and height  . The geoStarsLib has several methods to do this conversion.
. The geoStarsLib has several methods to do this conversion.
![\[\mathbf{\underline{geoStarsLib \; Method}}\]](form_19.png)

![\[\mathbf{\underline{Hirvonen \; and \;Moritz \; Method}} \]](form_21.png)
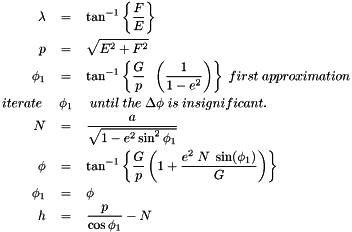
![\[\mathbf{\underline{Torge \; Method \;/\; Heiskanen \; and \; Moritz \;Method}} \]](form_23.png)

![\[\mathbf{\underline{Astronomical \; Almanac \; 2002 \; Method}} \]](form_25.png)

![\[\mathbf{\underline{Borkowski \; Method}} \]](form_27.png)
![\begin{eqnarray*} \lambda &=& \tan^{-1} \left\{ \frac{F}{E} \right\} \\ r &=& \frac {E}{\cos \lambda} \\ e_b &=& \frac{b G - \left( a^2 - b^2\right)}{a r} \\ f_b &=& \frac{b G + \left( a^2 - b^2\right)}{a r} \\ q &=& 2 \left(e_b^2 - f_b^2) \right) \\ p &=& \frac{4}{3} \left(e_b f_b + 1 \right) \\ d &=& p^3 + q^2 \\ v &=& \sqrt[3]{\sqrt{d} - q} - \sqrt[3]{\sqrt{d} + q} \\ g_b &=& \frac{\sqrt{e^2_b + v} + e_b}{2} \\ t &=& \sqrt{g_b^2 + \frac{f_b-vg_b}{2g_b-e_b} - g_b} \\ \phi &=& \tan^-1\left(\frac{a\left(1-t^2\right)}{2bt} \right) \\ h &=& \left(r-at\right)\cos\phi + \left(G-b \right)\sin\phi \\ \end{eqnarray*}](form_28.png)
![\[\mathbf{\underline{Vermeille \; Method}} \]](form_29.png)
![\begin{eqnarray*} p &=& \frac{E^2 +F^2}{a2} \\ q &=& G^2\frac{1-e^2}{a^2} \\ r &=& \frac{p+q-e^4}{6} \\ s &=& e^4 \frac{pq}{4r^3} \\ t &=& \sqrt[3]{1+s+\sqrt{s\left(2+s\right)}} \\ u &=& r\left(1+t+\frac{1}{t} \right) \\ v &=& \sqrt{u^2+e^4q} \\ w &=& e^2\frac{u+v-q}{2v} \\ k &=& \sqrt{u+v+w^2}-w \\ D &=& \frac{k\sqrt{E^2 +G^2}}{k+e^2} \\ \lambda &=& 2 \;tan^{-1} \frac{F}{E+\sqrt{E^2+F^2}} \\ \phi &=& 2 \;tan^{-1} \frac{G}{D+\sqrt{D^2+G^2}} \\ h &=& \frac{k+e^2-1}{k}\sqrt{D^2+G^2} \\ \end{eqnarray*}](form_30.png)
The modeling of the earth's magnetic field is called geomagnetism. The most current application of this model is magnetic declination - deflection of the compass needle off true north. The earth's magnetic field is in constant motion. Thus, a stable model needed to be developed so that one might be able to correct for the changes of the field in time.
By using the geomagnetic routines in this library, true north can be determined quite easily.
The geoStarsLib library uses the World Magnetic Model of 2010.
The following figure shows the magentic declination in all areas of the world.
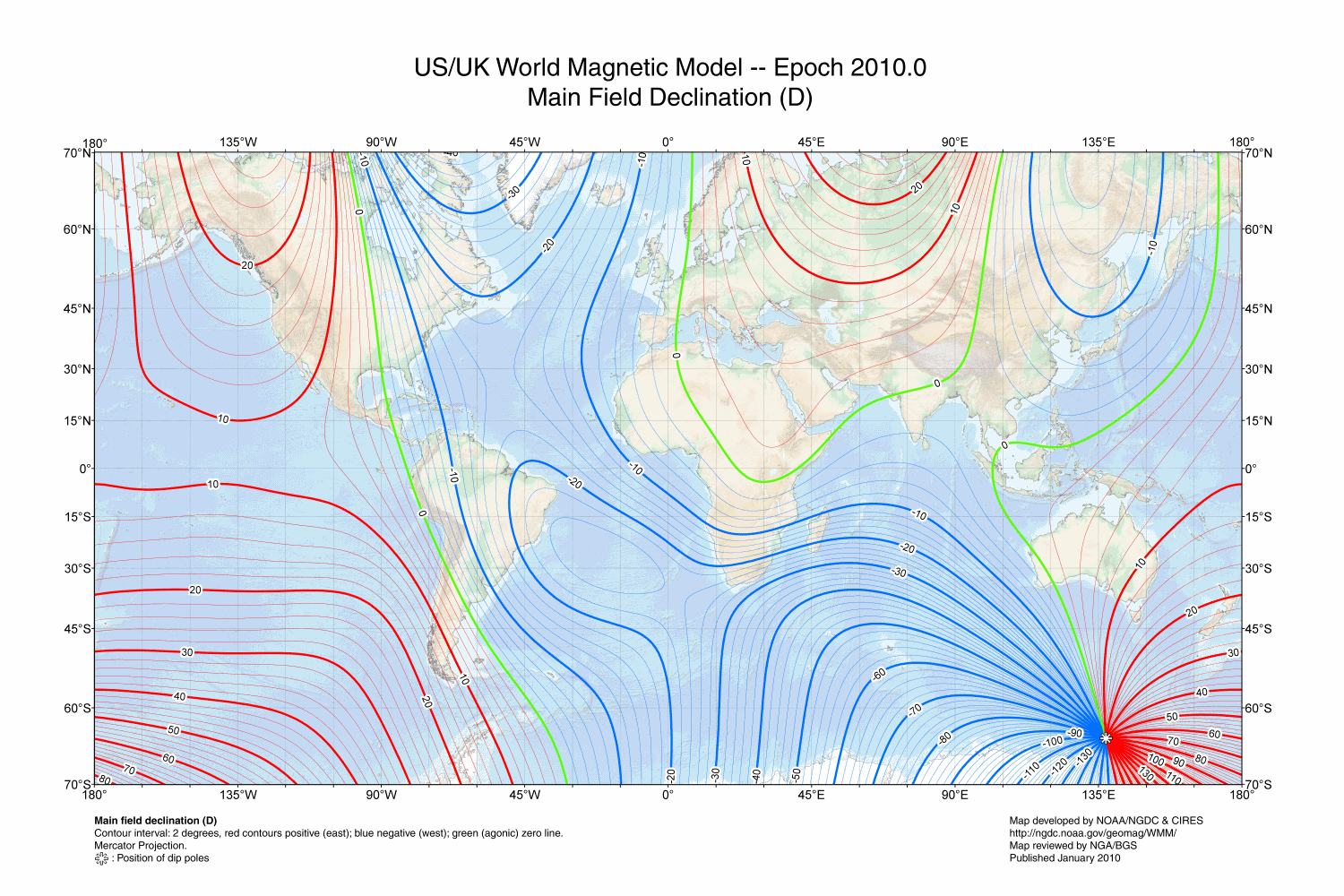
Since the magnetic field is always in flux, the WMM2010 discusses the annual rate of change and charts it as follows:
geoStarsLib.dll can be used with VB, VBA, and other programs that can access external DLL's. The DLL must be located in the path to be used with Excel. The file geoTest.bas is an example of how the DLL functions are called from VB. It tests the sun position at the current time. You must make sure that geo.bas is loaded in your project to provide the interface to the DLL.
All of the geoStarsLib routines can be called from Visual Basic using the Function and Call methods.
Follow this link for more information:
\ref HomeHere are some common questions:
 1.8.4
1.8.4